iOS平台上aa(见缝插针)游戏的简易实现

还记得那是2015年的6月的一场雨后（一场雨，把我困在这里……），老姐拿来了她在QQ空间里看到的一个有趣的游戏：见缝插针。（当时还没入移动开发这行，还是一个刚读大学的愣头青，不知道这是iOS平台上率先推出一款风靡全球的经典休闲游戏：aa）这个网页版的用户体验就没有移动端的感觉好了，不过这都是后来才知道的。诶，这游戏乍一看下不会觉得太难，然后你可能会很快地通过了前面几个很简单的关卡（我最初接触到的只有15关），然后你在8、9关左右可能就会第一次失败，然后很蛋疼的发现游戏又从第1关开始了。一两次还好，要是你好不容易克服“艰难险阻”来到了12、13关，再给你整这么一出，内心的阴影面积可想而知，摔手机的心情都有了！

在“入坑”之后，面对这些东西就不会只是纯粹地欣赏和玩乐了，而是总会下意识地思考这个效果可以兑现为怎样的一段代码。然后借由这个思考结果不断在开发工具里捣鼓摸索着，终于有一日灵光一闪，实验样品出来了。随即又因按捺不住内心的冲动，想要通过某种渠道写点什么东西来分享这么一个实践过程，于是就有了这么一篇文章：iOS平台上aa（见缝插针）游戏的简易实现。

知己知彼，百战不殆

玩过aa的朋友都知道，它的游戏逻辑是这样的：每一关你都有不同数量的“针”，中心的圆盘上初始状态可能就会有“针”已经插入就绪，不过这是为增加游戏难度而设计的。你的任务就是将你所在关卡中所持有的所有“针”插入到中心转动的圆盘上去（插入点是相对固定的），前提是不能与其他“针”相互接触，否则游戏宣告失败。为了不让你很快通关，后面的关卡理所当然难度会越来越大，比如圆盘转速增加、初始就绪“针”数和持有针数增加、顺逆时针变速转动（最坑的就是这一点，我在这上面载了不少跟头！），这里之所以叫做简易实现主要是因为Demo只是简单实现了游戏逻辑，没有设置多重关卡，取而代之的是所谓的无尽模式。

因为开始实践这个游戏时，我已经快要期末考试了，所以需要着手准备考试和实习的事情，没有太多的精力去设计游戏的美化和后继的关卡。当然，如果后面有机会的话，应该会有Demo2.0版本。

关于这个游戏的实现，我最开始的想法就是当你点击屏幕时，扩展中心圆盘（CAShapeLayer实例）的path属性，以达到最终“针”插在圆盘上的效果。对于“针”的动态移动过程，就可以创建一个过渡的“针”视图来等效代替。那么核心的问题就来了：我在扩展图层的路径时，怎么确定绘制的起始点和终点呢？因为在中心圆盘的旋转过程中，其上的个点也会随之一起做仿射变换。如果你在图层旋转时还是以圆盘静止时硬编码取到的起点和终点来确认绘制“针”的话，那么新绘制的“针”就会和之前“插上”的“针”重合在一起，导致的结果就是：无论你怎么“插针”，圆盘上看到的就只有一根“针”，虽然实际上它是很多“针”重叠在一起而表现出来的结果。

那么首要问题就是如何得到当前“针”的绘制起点和终点？

实践是检验真理的唯一标准

值得庆幸的是中心转轴是圆形的（故称之为圆盘），而且也只能是在圆形的情况下才能设计出aa这样的游戏效果。因为插针的起点和终点的计算依赖于圆形的中心到边界各点的距离相等这一性质，具体可以用如下两张图来表示坐标点的换算过程：

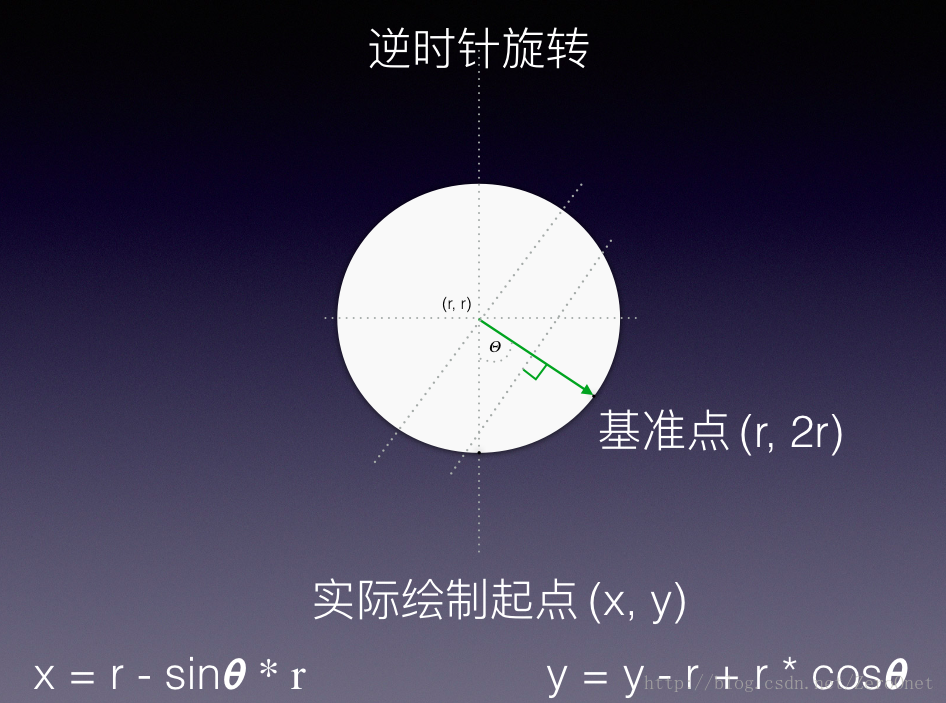
其中的基准点为在静止时“针”的插入点（对应于绘制“针”的起点），而终点可以通过相同的方法来实现换算，只不过半径r的值需要做出相应的调整。

那么实践所面临的问题又转向了如何取得在旋转过程中图层的旋转角度了，很不幸地说，Apple没有提供直接的API来获取这么一个值。在笔者实践了一些方法无果后，就决定在Stack Overflow去刷下存在感，问一下问题，结果就遇到了一些尴尬的事情！就把它当做是一个小插曲，分享给各位，望引以为戒！

无疑，在Ask question之前，你得先搜索相关问题是否有人已经提出，或许你就可以直接捡现成的了。这不，刚输入关键字就发现了可能的解决方法：

看一看问题描述：

看看回答：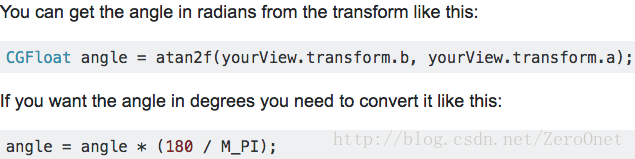

咦！好像有那么一回事，先拿来试下！………………… （此处略去100字的实践过程）结果发现，它只能计算旋转最终状态时的角度值，即如果别人不告诉你某个视图将要旋转多少角度，你可以这样来得到他预先设定值。计算结果显然是和XXView.transform.b、XXView.transform.a相关的，因为在设定结束后，相应的仿射变换也会随即生效。

问题没有得到解决，于是新的问题就有提出来的必要了：

完了之后，就被人“嘲笑”了，这是理由：

这是他把我的问题改版前后的对照结果：

唉！原谅我这个新手的不懂规矩啊！这也从一个侧面反映了Stack Overflow的专业性，也就难怪大神们都愿意在这里进行技术交流。下面是我的道谢：

很遗憾，到目前为止还没有任何人回答这个问题！真是大写的尴尬啊！所以在遇到问题时，向别人请教的同时自己也需要不断思考问题的解决方案。正所谓“自己动手，丰衣足食”。

其实，之前的回答已经告诉了我们答案，只是这里我们需要在动画过程中通过某种方式来获得类似于XXView.transform.b、XXView.transform.a这样的量。我们都知道的是要是涉及到动画的话，图层会将动画的过程交给presentationLayer（表现层）来完成。至于动画的初值和终值之间的中间值则由系统不断计算，并通过表现层来展示。说到这里就很明确了，我们在这里所涉及到的需求依据变颜色这段文字，所遇到的麻烦就迎刃而解了。

一直向前

既然我们选用的是图层，我们就需要知道它的transform属性是一个名为CATransform3D的结构体变量，而XXView的transform属性是一个名为CGAffineTransform的结构体变量。前者就自然没有a、b这样的成员变量，而是这样的一个矩阵结构：

struct CATransform3D
{
  CGFloat m11, m12, m13, m14;           
  CGFloat m21, m22, m23, m24;
  CGFloat m31, m32, m33, m34;
  CGFloat m41, m42, m43, m44;
};

其中的m14、m24、m34、m44只是作为矩阵的占位符，通常会将m14、m24、m34设置为0，m44设为1。其他分量的值对应于不同的场景，表示如下：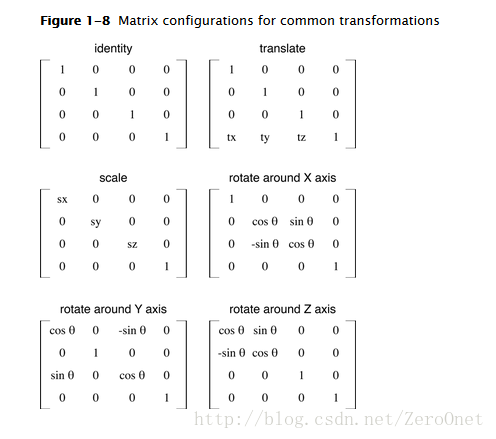

这个例子中我们是围绕z轴旋转的，我们就可以使用反正切变换函数参入实际参数m21、m22的值就可以实时地知道图层的当前旋转角度了，不过这肯定需要一些修正以适配于顺时针、逆时针的角度计算结果值域为0 ~ 2π（反正切计算结果以弧度制表示）：

//此方法为对外开放的方法，主要用于在不同旋转方向下，能够实时获取图层的旋转角度
- (CGFloat)transformAngleWithRotationDirection:(BOOL)clockwise {
    return clockwise ? [self transformRotationAngle] : 2.0f * M_PI - [self transformRotationAngle];
}

//此方法为私有方法，它所返回的值对于坐标变换计算有直接使用之便
- (CGFloat)transformRotationAngle {
	//这里其实可以用反正弦和反余弦来计算角度值
    CGFloat degreeAngle = - atan2f(self.presentationLayer.transform.m21, self.presentationLayer.transform.m22);
    
    if (degreeAngle < 0.0f) {
        degreeAngle += (2.0f * M_PI);
    }
    
    return degreeAngle;
}

借助于数学诱导公式，坐标的变换计算公式可以统一为如下形式：

- (CGPoint)convertPointWhenRotatingWithBenchmarkPoint:(CGPoint)point roundRadius:(CGFloat)radius {
    CGFloat rotationAngle = [self.presentationLayer transformRotationAngle];

    return CGPointMake(point.x + sinf(rotationAngle) * radius, point.y - radius + cosf(rotationAngle) * radius);
}

下面是最终的效果图：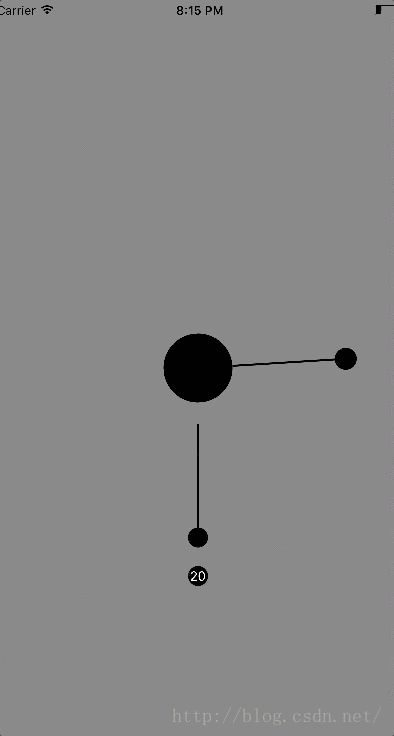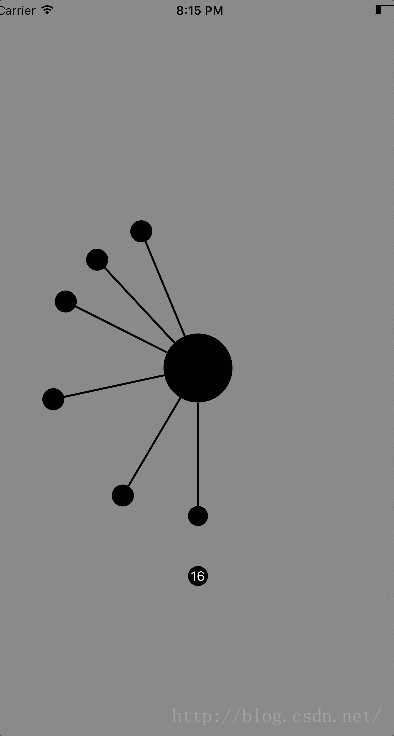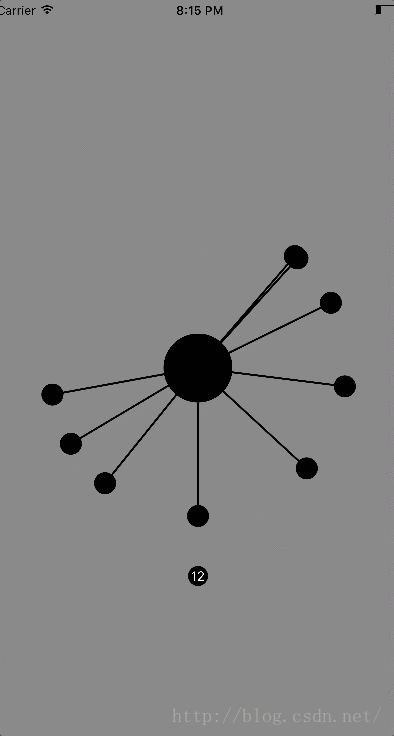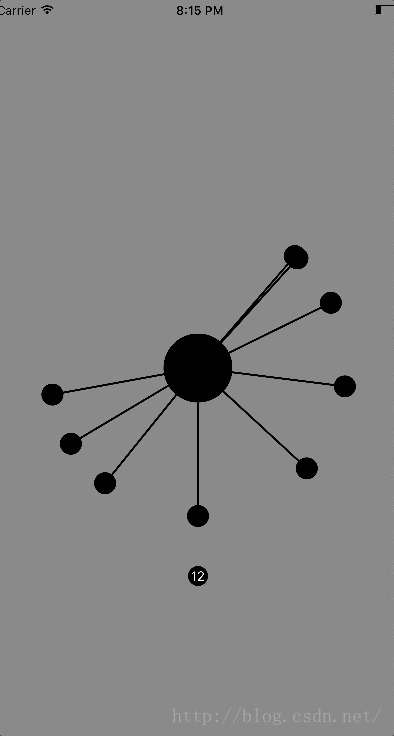

总结

虽然，在书写文章的时候给人的感觉思路是很明确的，且整个过程是连贯的，但是事实上在实践中走弯路甚至半途而废是不可避免的。拿这个Demo来说，在这之前动手写过一次的，但是那次可能因为技术的储备不够（到现在为止，网上依然找不到其他人在iOS平台上对这个游戏的实现Demo），半途而废了！但就在前几天，觉得技术提升与否需要通过是否能完成之前不能完成的任务来衡量。加上做别人没有做过的实践，总是会更有趣和更有挑战意义的，这不就是价值的体现吗？这里是Demo的下载地址，有兴趣的朋友可以下载下来看看，谢谢捧场！